Research overview
My research is rooted in the mathematical foundations of data science, with primary focuses on theory and algorithms for large-scale optimization problems from engineering, data sciences and machine learning for graphical data. Most of my research is in one of the following directions.
Distributed and decentralized optimization
I design communication networks and optimization algorithms in decentralized optimization and manage the trade-off between communication costs and convergence rate.First-order methods for large-scale systems
I design, analyze and implement proximal first-order methods for large-scale optimization problems.Nonlinear and nonconvex optimization with benign structure
I try to identify interesting problem and data structures and design efficient algorithms for these problems.Constrained stochastic optimization
For smooth nonlinear optimization problems, I study stochastic-gradient-based algorithms that can handle deterministic constraints.Machine learning for graphical data
I aim to build data-centric and robust graph representation models, especially with fairness and privacy concerns.
Distributed and decentralized optimization
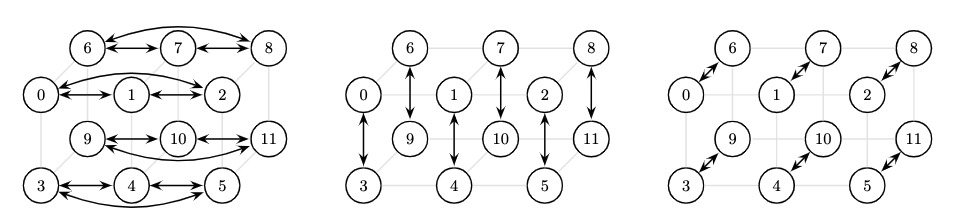
Distributed and decentralized methods allow computational agents to communicate over a network and to collaboratively solve an optimization problem. This area has received increasing attention, partially due to the recent interests in federated learning with privacy concerns. My research involves the design and analysis of distributed algorithms as well as the network topology in decentralized optimization.
 |
Selected publications:
A general framework for an exact decentralized optimization problem under time-varying networks
E. D. H. Nguyen, B. Ying, W. Yin, and X. Jiang, 2024+Sparse factorization of the square all-ones matrix of arbitrary order
X. Jiang, E. D. H. Nguyen, C. A. Uribe, and B. Ying, 2024On graphs with finite-time consensus and their use in gradient tracking
E. D. H. Nguyen, X. Jiang, B. Ying, and C. A. Uribe, 2023
Structured nonlinear and nonconvex optimization
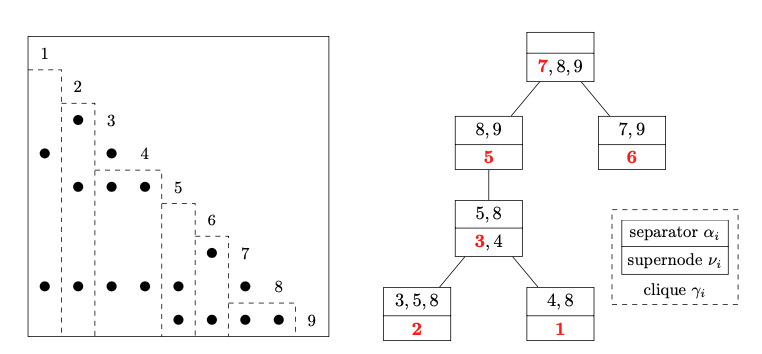
Exploiting problem and data structure is important in both convex and nonconvex optimization. Convex conic optimization, for example, is the basis for general-purpose solvers as well as an important modeling tool for various applications. On the other hand, for certain nonconvex optimization problems, specific problem structure could be leveraged to find a global optimum. My research in this direction exploits interesting structures in the positive semidefinite (PSD) matrix cone, the monotone cone, difference-of-convex (DC) programming, etc.
 |
Selected publications:
Local linear convergence of the alternating direction method of multipliers for semidefinite programming under strict complementarity
S. Kang, X. Jiang, and H. Yang, 2025Minimum-rank positive semidefinite matrix completion with chordal patterns and applications to semidefinite relaxations
X. Jiang, Y. Sun, M. S. Andersen, and L. Vandenberghe, 2023Bregman primal-dual first-order method and application to sparse semidefinite programming
X. Jiang, and L. Vandenberghe, 2022
Proximal methods with Bregman distances
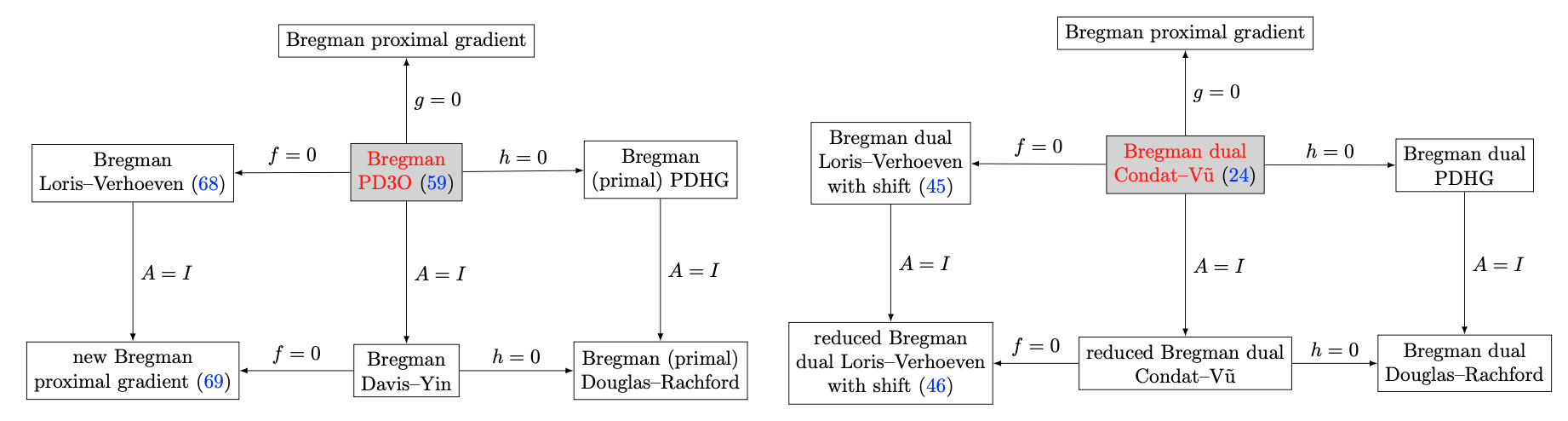
Proximal methods have become a standard tool for solving nonsmooth, constrained, large-scale or distributed optimization probelms. To further improve the efficiency in computation of proximal operators, I am particularly interested in generalized proximal operators based on Bregman distances. Carefully designed Bregman proximal operators can better match the structure of the problem, thus improving the convergence rate of the proximal algorithms. A Bregman proximal operator can also be easier to compute than its Euclidean counterpart, thereby reducing the per-iteration complexity of a proximal algorithm.
 |
Selected publications
Primal-dual proximal methods for self-dual conic linear programs
X. Jiang, J. Shao, and L. Vandenberghe, 2024+Bregman three-operator splitting methods
X. Jiang, and L. Vandenberghe, 2023Bregman primal-dual first-order method and application to sparse semidefinite programming
X. Jiang, and L. Vandenberghe, 2022
Constrained stochastic optimization
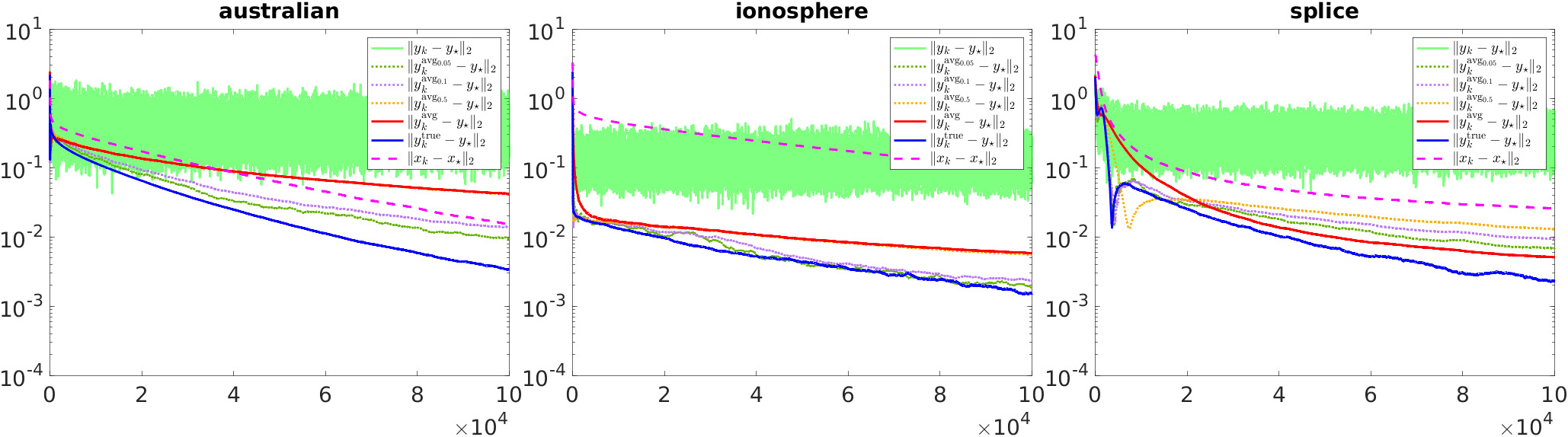
My research focuses on the design, analysis and implementation of efficient and reliable algorithms for solving large-scale nonlinear optimization problems, especially when only stochastic estimates of objective gradients (rather than true gradients) are accessible.
 |
Selected publications:
Single-loop deterministic and stochastic interior-point algorithms for nonlinearly constrained optimization
F. E. Curtis, X. Jiang, and Q. Wang, 2024Almost-sure convergence of iterates and multipliers in stochastic sequential quadratic optimization
F. E. Curtis, X. Jiang, and Q. Wang, 2023
Machine learning for graphical data
My research in this direction aims at building a data-centric, scalable, and robust graph representation model. My recent research interests involve graph representation models with fairness and privacy concerns.
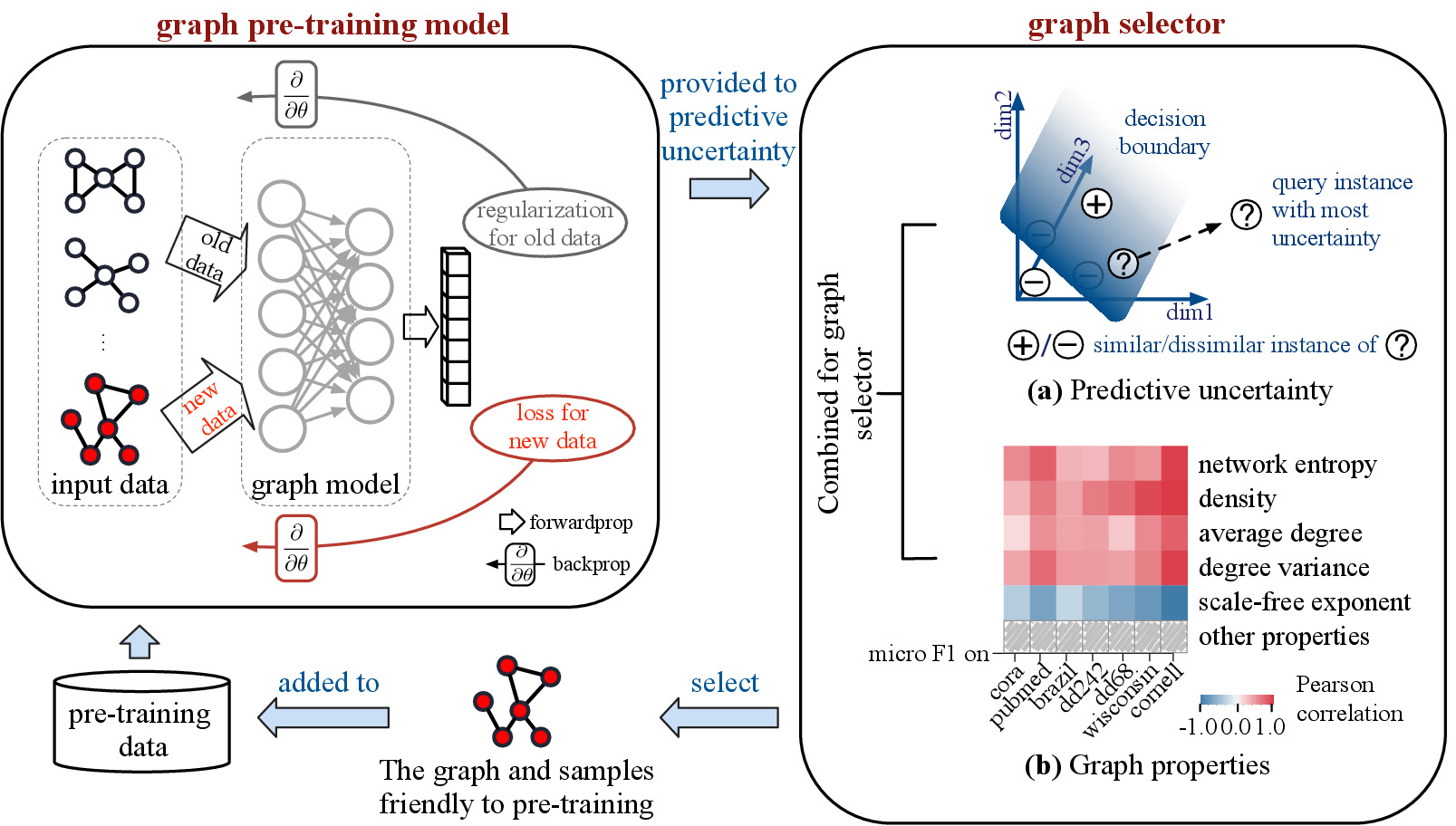 |
Selected publications:
Extracting training data from molecular pre-trained models [NeurIPS’24]
R. Huang, J. Xu, Z. Yang, X. Si, X. Jiang, H. Yuan, C. Wang, and Y. YangCan modifying data address graph domain adaptation? [KDD’24]
R. Huang, J. Xu, X. Jiang, R. An, and Y. YangBetter with less: A data-active perspective on pre-training graph neural networks [NeurIPS’23]
J. Xu, R. Huang, X. Jiang, Y. Cao, C. Yang, C. Wang, and Y. Yang